Момент сил відносно осі обертання: основні поняття, формули, приклад розв\'язання задачі

Коли вирішують завдання на переміщення об\'єктів, то в ряді випадків нехтують їх просторовими розмірами, вводячи поняття матеріальної точки. Для іншого типу завдань, в яких розглядаються покояться або обертові тіла, важливо знати їх параметри та точки прикладання зовнішніх сил. У цьому випадку мова йде про момент сил відносно осі обертання. Розглянемо це питання в статті. Поняття про момент сили

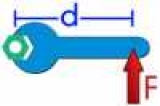
Перед тим як наводити формули моменту сили відносно нерухомої осі обертання, необхідно пояснити, про яке явище піде мова. Нижче дан малюнок, на якому зображено гайковий ключ довжиною d, до кінця його прикладена сила F. Неважко уявити, що результатом її впливу буде обертання ключа проти годинникової стрілки і відкручування гайки.

Згідно з визначенням, момент сили відносно осі обертання являє собою твір плеча (d в даному випадку) на силу (F), тобто можна записати наступний вираз: M = d*F. Відразу ж слід застерегти, що наведена формула записана в скалярному вигляді, тобто вона дозволяє розрахувати абсолютне значення моменту M. Як видно з формули, одиницею вимірювання даної величини є ньютон на метр (Н*м). Момент сили - векторна величина

Як вище було зазначено, момент M насправді являє собою вектор. Для пояснення цього твердження розглянемо інший малюнок.

Тут ми бачимо важіль довжиною L, який закріплений на осі (показано стрілкою). До його кінця прикладена сила F під кутом ?. Неважко собі уявити, що ця сила буде викликати підйом важеля. Формула для моменту у векторній формі в цьому випадку запишеться так: M = L*F, тут риска над символом означає, що розглянута величина - це вектор. Слід пояснити, що L спрямований від осі обертання до точки прикладання сили F.

Наведений вираз є векторним добутком. Його результуючий вектор (M) буде направлений перпендикулярно до площини, утвореної L і F. Для визначення напрямку моменту M існують кілька правил (правої руки, буравчика). Щоб не заучувати їх і не плутатися в порядку множення векторів L і F (від нього залежить напрямок M), слід запам\'ятати одну просту річ: момент сили буде спрямований таким чином, що якщо дивитися з кінця вектора, то впливає сила F буде обертати важіль проти годинникової стрілки. Це напрямок моменту умовно прийнято за позитивне. Якщо ж система здійснює обертання годинникової стрілки, отже, результуючий момент сил має від\'ємне значення.

Таким чином, у розглянутому випадку з важелем L величина M спрямована вгору (від малюнка до читача).

У скалярної формі формула для моменту запишеться у вигляді: M = L*F*sin(180-?) або M = L*F*sin(?) (sin(180-?) = sin(?)). Відповідно до визначення синуса, можна записати рівність: M = d*F, де d = L*sin(?) (див. малюнок і відповідний прямокутний трикутник). Остання формула є аналогічною тій, яка була наведена в попередньому пункті.

Проведені вище обчислення демонструють, як працювати з векторними і скалярними величинами моментів сил, щоб не допустити помилок. Фізичний зміст величини M

Оскільки два розглянутих у попередніх пунктах випадки пов\'язані з обертальним рухом, то можна здогадатися, який сенс несе момент сили. Якщо сила, що діє на матеріальну точку, є мірою збільшення швидкості лінійного переміщення останньої, то момент сили - це міра її обертальної здатності стосовно до розглянутої системи.

Наведемо наочний приклад. Будь-яка людина відкриває двері, взявшись за ручку. Також це можна зробити, якщо штовхнути двері в зоні ручки. Чому ніхто не відкриває її, штовхаючи в області петель? Дуже просто: чим ближче до петель прикладена сила, тим важче відкрити двері, і навпаки. Висновок попереднього речення випливає з формули для моменту (M = d*F), звідки видно, що при M = const величини d і F перебувають у зворотній залежності.

Момент сили - величина адитивна

В усіх розглянутих вище випадках мала місце лише одна діюча сила. При вирішенні реальних завдань справа йде набагато складніше. Зазвичай на системи, які обертаються або знаходяться в рівновазі, діють декілька сил кручення, кожна з яких створює свій момент. У цьому випадку рішення задач зводиться до знаходження сумарного моменту сил відносно осі обертання.

Сумарний момент знаходиться шляхом звичайної суми окремих моментів для кожної сили, проте, слід не забувати використовувати правильний знак для кожного з них. Приклад розв\'язання задачі

Для закріплення отриманих знань пропонується вирішити наступну задачу: необхідно обчислити сумарний момент сили для системи, зображеної на малюнку нижче.

Ми бачимо, що на важіль довжиною 7 м діють три сили (F1, F2, F3), причому вони мають різні точки програми щодо осі обертання. Оскільки напрям сил перпендикулярно важелю, то немає необхідності застосовувати векторне вираз для моменту кручення. Можна розрахувати сумарний момент M, використовуючи скалярну формулу і не забуваючи про взяття потрібного знака. Оскільки сили F1 і F3 прагнуть повернути важіль проти годинникової стрілки, а F2 - за годинниковою стрілкою, то момент обертання для перших буде позитивним, а для другої - негативним. Маємо: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. тобто сумарний момент є позитивним і направлений вгору (на читача). Автор: Валерій Савельєв 29 Вересня, 2018

Категория: Новости