Апофема піраміди. Формули для апофемы правильної трикутної піраміди

Опубликованно 01.02.2019 09:35

Піраміда - це просторовий полиэдр, або многогранник, який зустрічається в геометричних задачах. Основними властивостями цієї фігури є її об\'єм і площа поверхні, які обчислюються із знання будь-яких двох її лінійних характеристик. Однією з таких характеристик є апофема піраміди. Про неї піде мова в статті. Фігура піраміда

Перш ніж наводити визначення апофемы піраміди, познайомимося з самою фігурою. Піраміда являє собою багатогранник, який утворений одним n-вугільним підставою і n трикутниками, складовими бічну поверхню фігури.

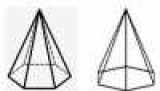
Кожна піраміда має вершину - точку з\'єднання всіх трикутників. Перпендикуляр, проведений із цієї вершини до основи, називається висотою. Якщо висота перетинає в геометричному центрі підстава, то фігура називається прямою. Піраміда пряма, що має равностороннее основа, називається правильною. На малюнку показана піраміда з шестикутним підставою, на яку дивляться з боку грані і ребра.

Апофема правильної піраміди

Її також називають апотемой. Під нею розуміють перпендикуляр, проведений з вершини піраміди на стороні підстави фігури. За своїм визначенням цей перпендикуляр відповідає висоті трикутника, який утворює бічну грань піраміди.

Оскільки ми розглядаємо правильну піраміду з n-вугільним підставою, то всі n апофем для неї будуть однаковими, оскільки такими є рівнобедрені трикутники бічній поверхні фігури. Зауважимо, що однакові апофемы є властивістю правильної піраміди. Для фігури загального типу (похилій з неправильним n-кутником) всі n апофем будуть різними.

Ще однією властивістю апофемы піраміди правильної є те, що вона одночасно є висотою, медіаною і бісектрисою відповідного трикутника. Це означає, що вона ділить його на два однакових прямокутних трикутника.

Трикутна піраміда і формули для визначення її апофемы

У будь правильній піраміді важливими лінійними характеристиками є довжина сторони її основи, бічне ребро b, висота h і апофема hb. Ці величини один з одним пов\'язані відповідними формулами, які можна отримати, якщо накреслити піраміду і розглянути необхідні прямокутні трикутники.

Правильна трикутна піраміда складається з 4 трикутних граней, причому одна з них (підстава) має бути обов\'язково рівносторонньою. Решта є равнобедренными в загальному випадку. Апофему трикутної піраміди можна визначити через інші величини за такими формулами:

hb = ?(b2 - a2/4);

hb = ?(a2/12 + h2)

Перше з цих виразів справедливо для піраміди з будь-яким правильним підставою. Другий вираз характерно виключно для трикутної піраміди. Воно показує, що апофема завжди більше висоти фігури.

Не слід плутати апофему піраміди з такою для багатогранника. В останньому випадку апофемой називається перпендикулярний відрізок, проведений на стороні багатогранника з його центру. Наприклад, апофема рівностороннього трикутника дорівнює ?3/6*a.

Завдання на обчислення апофемы

Нехай дана правильна піраміда з трикутником в підставі. Необхідно обчислити її апофему, якщо відомо, що площа трикутника дорівнює 34 см2, а сама піраміда складається з 4 однакових граней.

У відповідності з умовою задачі ми маємо справу з тетраедром, що складається з рівносторонніх трикутників. Формула площі для однієї грані має вигляд:

S = ?3/4*a2

Звідки отримуємо довжину сторони a:

a = 2*?(S/?3)

Для визначення апофемы hb скористаємося формулою, що містить бічне ребро b. У розглянутому випадку його довжина дорівнює довжині підстави, маємо:

hb = ?(b2 - a2/4) = ?3/2*a

Підставляючи значення a через S, отримаємо кінцеву формулу:

hb = ?3/2*2*?(S/?3) = ?(S*?3)

Ми отримали просту формулу, в якій апофема піраміди залежить тільки від площі її основи. Якщо підставити значення S з умови задачі, то отримаємо відповідь: hb ? 7,674 див. Автор: Валерій Савельєв 22 Листопада, 2018

Категория: Новости