Шестикутна призма та її основні характеристики

Опубликованно 06.03.2019 14:10

Вивченням призм займається просторова геометрія. Найважливішими їх характеристиками є укладений в них обсяг, площа поверхні і число складових елементів. У статті розглянемо всі ці властивості для шестикутної призми. Про який призмі піде мова?

Шестикутна Призма - це фігура, утворена двома багатокутниками, що мають шість сторін і шість кутів, і шістьма параллелограммами, що з\'єднують зазначені шестикутники в єдине геометричне освіта.

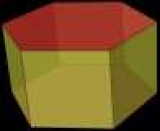
На малюнку зображено приклад цієї призми.

Відзначений червоним кольором шестикутник називається підставою фігури. Очевидно, що число її підстав дорівнює двом, причому обидва вони ідентичні. Жовто-зеленуваті грані призми називаються її бічними сторонами. На малюнку вони представлені квадратами, але в загальному випадку вони є параллелограммами.

Шестикутна призма може бути похилій і прямий. У першому випадку кути між підставою і бічними сторонами не є прямими, в другому вони дорівнюють 90o. Також ця призма може бути правильною і неправильною. Правильна шестикутна призма обов\'язково повинна бути прямою і мати правильний шестикутник в підставі. Наведена вище призма на малюнку цим вимогам задовольняє, тому вона називається правильною. Далі в статті будемо вивчати тільки її властивості, як загальний випадок. Елементи

Для будь-якої призми головними її елементами є ребра, грані, вершини. Шестикутна призма не є винятком. Наведений вище малюнок дозволяє порахувати кількість цих елементів. Так, граней або сторін ми отримуємо 8 (дві підстави і шість бічних паралелограмів), число вершин становить 12 (по 6 вершин для кожної підстави), кількість ребер шестикутної призми дорівнює 18 (шість бічних і 12 для підстав).

У 1750-ті роки Леонард Ейлер (швейцарський математик) встановив для всіх поліедрів, до яких ставиться призма, математичний зв\'язок між числами зазначених елементів. Цей зв\'язок має вигляд:

число ребер = число граней + число вершин - 2.

Зазначені вище цифри задовольняють цій формулі. Діагоналі призми

Всі діагоналі шестикутної призми можна розділити на два типу: ті, які лежать в площинах її граней; ті, які належать всьому об\'єму фігури.

Малюнок нижче показує всі ці діагоналі.

Видно, що D1 - це діагональ бічної сторони, D2 і D3 - діагоналі всій призми, D4 D5 - діагоналі основи.

Довжини діагоналей бічних сторін між собою рівні. Обчислити її легко, використовуючи всім відому теорему Піфагора. Позначимо символом a довжину сторони шестикутника, символом b - довжину бічного ребра. Тоді діагональ має довжину:

D1 = ?(a2 + b2).

Діагональ D4 також легко визначається. Якщо згадати, що правильний шестикутник вписується в коло радіусом a, D4 діаметр цього кола, тобто отримаємо наступну формулу:

D4 = 2*a.

Діагональ D5 заснування знайти дещо складніше. Для цього слід розглянути рівносторонній трикутник ABC (див. рис.). Для нього AB = BC = a, кут ABC дорівнює 120o. Якщо з цього кута опустити висоту (вона ж буде бісектрисою і медіаною), тоді половина підстави AC буде дорівнює:

AC/2 = AB*sin(60o) = a*?3/2.

Сторона AC є діагоналлю D5, тому отримуємо:

D5 = AC = ?3*a.

Тепер залишається знайти діагоналі D2 і D3 правильної шестикутної призми. Для цього потрібно побачити, що вони є гипотенузами відповідних прямокутних трикутників. Скориставшись теоремою Піфагора, отримуємо:

D2 = ?(D42 + b2) = ?(4*a2 + b2);

D3 = ?(D52+ b2) = ?(3*a2+ b2).

Таким чином, самою великою діагоналлю для будь-яких значень a і b є D2. Площа поверхні

Щоб зрозуміти, про що йде мова, найпростіше розглянути розгортку цієї призми. Вона показана на малюнку.

Видно, що для визначення площі всіх сторін розглянутої фігури необхідно розрахувати окремо площа чотирикутника і площа шестикутника, потім помножити їх на відповідні цілі числа, рівні кількості кожного n-кутника в призмі, і скласти отримані результати. Шестикутників 2, 6 прямокутників.

Для площі прямокутника отримуємо:

S1 = a*b.

Тоді площа бічної поверхні дорівнює:

S2 = 6*a*b.

Для визначення площі шестикутника найпростіше скористатися відповідною формулою, яка має вигляд:

Sn = n/4*a2*ctg(pi/n).

Підставляючи в цей вираз число n дорівнює 6, отримуємо площа одного шестикутника:

S6 = 6/4*a2*ctg(pi/6) = 3*?3/2*a2.

Цей вираз слід помножити на два, щоб отримати площа підстав призми:

Sos = 3*?3*a2.

Залишається скласти Sos і S2, щоб отримати повну площу поверхні фігури:

S = Sos + S2 = 3*?3*a2 + 6*a*b = 3*a*(?3*a + 2*b). Об\'єм призми

Після того як було отримано формулу для площі шестикутного підстави, обчислити обсяг, укладений у розглянуту призму, простіше простого. Для цього слід лише помножити площу однієї підстави (шестикутника) на висоту фігури, довжина якої дорівнює довжині бічного ребра. Отримуємо формулу:

V = S6*b = 3*?3/2*a2*b.

Зазначимо, що твір підстави на висоту дає значення обсягу абсолютно будь призми, включаючи похилу. Однак в останньому випадку розрахунок висоти ускладнюється, оскільки вона вже не буде дорівнює довжині бічного ребра. Що стосується правильної шестикутної призми, то значення її обсягу є функцією двох змінних: сторін a і b. Автор: Валерій Савельєв 11 Листопада, 2018

Категория: Новости